Sistemas de masa variable (I). Cohetes

Formulación discreta de las ecuaciones del movimiento de un cohete.

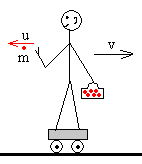Un cohete expulsa una fracción m de su combustible a intervalos de tiempos fijos (por ejemplo, cada segundo), con una velocidad u respecto del cohete. Este es un problema similar al de un patinador de masa M en una pista de hielo que arroja repetidamente bolas de masa m con velocidad constante u respecto del patinador.

Supondremos que el cohete está en el espacio exterior y por tanto, no actúa ninguna fuerza exterior sobre el mismo. Para calcular la velocidad del cohete a medida que va expulsando el combustible aplicamos el principio de conservación del momento lineal.

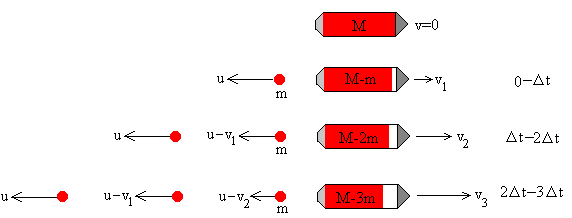
El cohete tiene una masa M que incluye la carga útil, el combustible y la masa del depósito que lo contiene. Supondremos que el cohete expulsa n fracciones de combustible de masa m a intervalos fijos de tiempo, es decir, en los instantes 0, Dt, 2·Dt...(n-1) ·Dt, alcanzando la velocidad en v₁, v₂, ....v_n, tal como se muestra en la figura.

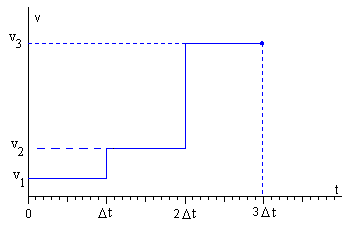
Velocidad del cohete

1. En el intervalo (0-Dt)

En el instante inicial t=0, expulsa una fracción m de combustible con una velocidad u respecto del cohete. El cohete pierde una masa m y adquiere una velocidad v₁. Si el cohete estaba inicialmente en reposo, su momento lineal es cero. Por tanto, la suma del momento lineal del cohete más el momento lineal del combustible expulsado debe dar cero.

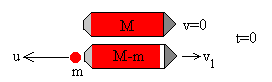(M-m)v1+m(-u)=0

El cohete se moverá con velocidad constante v₁ en el intervalo de tiempo 0-Dt. La fracción m del combustible expulsado se moverá con velocidad constante –u.

2. En el intervalo (Dt-2Dt)

En el instante Dt, el cohete expulsa otra fracción m de combustible con velocidad u respecto del cohete o v₁-u respecto de Tierra. El cohete pierde otra masa m y adquiere una velocidad v₂.
El momento lineal inicial del cohete (M-m)v₁ es igual al momento final del cohete más el de la fracción m del combustible expulsado.

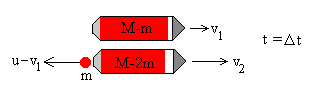(M-2m)v2+m(v1-u)= (M-m)v1

El cohete se moverá con velocidad constante v₂ en el intervalo de tiempo Dt -2Dt. La fracción m del combustible expulsado se moverá con velocidad constante v₁-u.

3. En el intervalo (2Dt-3Dt)

En el instante 2Dt, el cohete expulsa otra fracción m de combustible con velocidad u respecto del cohete o v₂-u respecto de Tierra. El cohete pierde otra masa m y adquiere una velocidad v₃. Aplicando el principio de conservación del momento lineal, despejamos v₃.

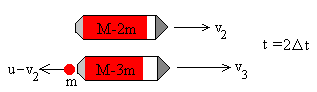(M-3m)v3+m(v2-u)= (M-2m)v2

El cohete se moverá con velocidad constante v₃ en el intervalo de tiempo 2Dt -3Dt. La fracción m del combustible expulsado se moverá con velocidad constante v₂-u.

4. En el intervalo ((n-1)Dt-nDt)

En el instante (n-1)Dt, el cohete expulsa la última fracción m de combustible con velocidad u respecto del cohete o v_n-1-u respecto de Tierra. El cohete pierde otra masa m y adquiere una velocidad v_n.

El cohete se moverá con velocidad constante v_n en a partir del instante t=(n-1)D t. La última fracción m del combustible expulsado se moverá con velocidad constante v_n-1-u.

Momento lineal

En el intervalo de tiempo comprendido entre (i-1)·Dt -i·Dt el momento lineal del cohete es

P_c=(M-i·m)v_i

El momento lineal del combustible expulsado, como podemos comprobar en la primera figura es

P_g=m(-u)+m(v₁-u)+m(v₂-u)+…m(v_i-1-u)

La conservación del momento lineal del sistema aislado formado por el cohete y el combustible que expulsa, exige que ambos momentos sean iguales y de sentido contrario. P_c+P_g=0.

Energía

La energía final del sistema, es la suma de la energía cinética del cohete E_c con velocidad final v_n, y la energía cinética E_g de las fracciones de masa m de combustible expulsados con velocidad (-u), (v₁-u), (v₂-u)… (v_n-1-u), respectivamente.

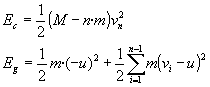
Desplazamiento

• El desplazamiento en el intervalo de tiempo (0-Dt) es x₁=v₁·Dt
• El desplazamiento en el intervalo de tiempo (Dt-2Dt), vale x₂=v₂·Dt
• El desplazamiento en el intervalo de tiempo (2Dt-3Dt), vale x₃=v₃·Dt

El desplazamiento total en el intervalo de tiempo (0- n·Dt) será

Del modelo discreto al continuo

El paso del modelo discreto al modelo continuo, que veremos en la siguiente página, implica incrementar el número n de fracciones de combustible de modo que la masa m de cada fracción sea cada vez más reducida. En el límite, cuando n tienda a infinito, la masa de cada fracción será una cantidad infinitesimal dm. Vamos a comparar las predicciones del modelo discreto frente a las del modelo continuo.

La masa inicial M es la suma de la carga útil, más el combustible y más la masa del recipiente que será proporcional a la masa del combustible que contiene

masa inicial  M  =carga útil+(1+r) ·combustible.

donde r es del orden del 5% ó 0.05.

Tomaremos el intervalo de tiempo Dt =1 s. De modo que, la primera fracción de combustible se expulsa en el instante t=0, la segunda en el instante t=1 s., la tercera en el instante t=2 s, y así sucesivamente. El combustible se agota en el instante t=(n-1) s.

Ejemplo 1:

• Combustible en el cohete, 9000 kg
• Carga útil que transporta, 800 kg.
• Número de fracciones, 3.

La masa inicial del cohete es (carga útil+combustible+masa del depósito)

M=800+1.05·9000=10250 kg.

La masa de cada fracción de combustible es m=9000/3=3000 kg, y se expulsan en los instantes t=0, t=1, y t=2 s.

La velocidad con la que se expulsa cada una de las fracciones es u=2000 m/s constante respecto del cohete, y está fijada en el programa interactivo.

Modelo discreto

Las velocidades del cohete en los intervalos de tiempo que se indican son

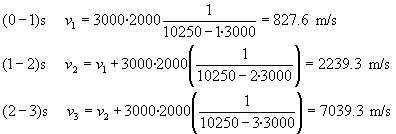
Intervalo (s)	Masa del cohete (kg)	Velocidad cohete (m/s)	Velocidad del combustible (m/s)
0-1	10250-3000	827.6	-2000
1-2	10250-2·3000	2239.3	827.6-2000
2-3	10250-3·3000	7039.3	2239.3-2000

1. Desplazamiento del cohete en el intervalo de (0- 3) s es el área bajo la curva escalonada.

x=827.6·1+2239.3·1+7039.3·1=10106.3 m.

2. Momento lineal final del cohete:

P_c=(10250-3·3000)·7039.3=8799188.6 kg·m/s

Momento lineal final de los gases expulsados:

P_g=3000·(-2000)+3000·(827.6-2000)+3000·(2239.3-2000)=-8799188.6 kg·m/s.

3. Energía del cohete:

E_c=(10250-3·3000)·7039.3²/2=3.097·10¹⁰ J

Energía de los gases expulsados:

E_g=3000·(-2000)²/2+3000·(827.6-2000)²/2+3000·(2239.3-2000)²/2=8.148·10⁹ J

La energía total necesaria para que el cohete alcance la velocidad final de 7039.3 m/s es la suma de las dos contribuciones.

E= E_c+ E_g=3.912·10¹⁰ J

Modelo continuo.

En la formulación continua, se queman 3000 kg de combustible cada segundo, D=3000 kg/s, resultando

• Velocidad final de v=4208 m/s
• Desplazamiento en el intervalo de tiempo (0-3)s es, x=4246 m.

Como vemos hay una gran diferencia entre las predicciones de ambos modelos

Ejemplo 2:

• Combustible en el cohete 9000 kg
• Carga útil que transporta 800 kg.
• Número de fracciones 9.

La masa inicial del cohete es (carga útil+combustible+masa del depósito)

M=800+1.05·9000=10250 kg.

La masa de cada fracción de combustible es m=9000/9=1000 kg, y se expulsan en los instantes t=0, t=1, ... t=8 s.

La velocidad de expulsión de cada una de las fracciones es de u=2000 m/s respecto del cohete, y está fijada en el programa interactivo.

Modelo discreto

Las velocidades del cohete en los intervalos de tiempo que se indican son

Intervalo (s)	Masa del cohete (kg)	Velocidad cohete (m/s)	Velocidad del combustible (m/s)
0-1	9250	216.2	-2000
1-2	8250	458.6	216.2-2000
2-3	7250	734.5	458.6-2000
3-4	6250	1054.5	734.5-2000
4-5	5250	1435.5	1054.5-2000
5-6	4250	1906.0	1435.5-2000
6-7	3250	2521.4	1906.0-2000
7-8	2250	3410.3	2521.4-2000
8-9	1250	5010.3	3410.3-2000

1. El desplazamiento total del cohete en el intervalo (0-9) s es x=16747.4 m

2. El momento lineal final del cohete es P_c=6262895.8 kg·m/s

El momento lineal final del combustible expulsado es P_g=-6262895.8 kg·m/s

3. La energía cinética del cohete es E_c=1.57·10¹⁰ J

La energía cinética del combustible expulsado es E_g=7.32 10⁹ J.

La energía total es E= E_c+ E_g=2.30·10¹⁰ J.

Modelo continuo

En la formulación continua, se queman 1000 kg de combustible cada segundo, D=1000 kg/s, resultando

• Velocidad final de v=4208 m/s.
• Desplazamiento en el intervalo de tiempo (0-9) s es, x=12740 m.

Los resultados del modelo discreto se van acercando a los del modelo continuo.

Fijarse que en el modelo continuo, la velocidad final del cohete es independiente de D, la cantidad de combustible quemado en la unidad de tiempo.