Aplicando una fuerza sobre una rueda

En el capítulo de dinámica se ha estudiado la fuerza de rozamiento y se ha afirmado que la fuerza de rozamiento se opone al movimiento del cuerpo. El sentido de dicha fuerza es opuesto al de la velocidad. Hemos visto como esta fuerza de rozamiento dinámica produce un trabajo negativo que hace que disminuya la energía total de la partícula.

Cuando un cuerpo rueda sin deslizar, la fuerza de rozamiento estática no produce trabajo alguno. Esta fuerza como vamos a ver puede tener el sentido del movimiento del centro de masa o el sentido opuesto.

Movimiento de un disco al que se le aplica una fuerza horizontal

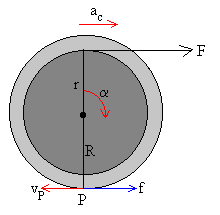
Supongamos que una fuerza externa F actúa a una distancia r<R por encima del centro de masas de una rueda. El punto P de contacto entre la rueda y el plano tiende a deslizar. Existe en dicho punto una fuerza de rozamiento F_r (estática) con un valor límite m _eN, que actúa en P para oponerse a que dicho punto (o línea de contacto) deslice. N es la reacción del plano sobre la rueda.

Movimiento de rodar sin deslizar

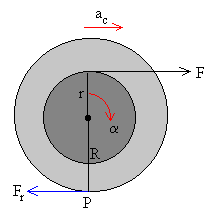Esta fuerza de rozamiento Fr se puede calcular a partir de las ecuaciones del movimiento Dinámica de la traslación del c.m. F-Fr=m·ac Dinámica de rotación alrededor de un eje que pasa por el c.m. F·r+Fr·R=Ic·a Además, de la condición de rodar (sin deslizar) ac=a ·R

Consideremos que el cuerpo que rueda es un cilindro o un disco de masa m y de radio R, cuyo momento de inercia respecto de a su eje de simetría es I_c=mR²/2,

Resolviendo las ecuaciones anteriores, obtenemos

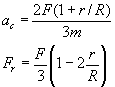
En la figura se muestra el vector F_r cuando r=0, r=R/2 y r=R.

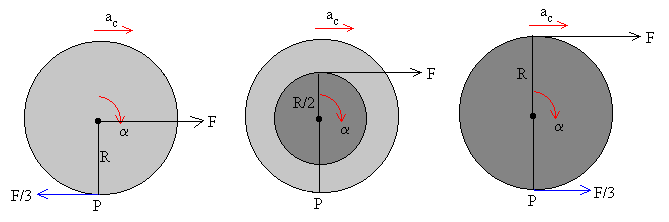
Para que la rueda se mantenga rodando sin deslizar se debe de cumplir que el valor absoluto de la fuerza de rozamiento estático F_r sea menor que el valor límite m_eN

|F_r|£ m_eN

con N=mg. Si el coeficiente de rozamiento estático µ_e es tal que

El cilindro rodará sin deslizar. En caso contrario, el cilindro rodará y deslizará a la vez bajo la acción de la fuerza F. Analicemos esta situación

Movimiento de rodar deslizando

Pueden ocurrir dos casos

• Si a_c>a R, entonces v_P>0. La fuerza de rozamiento dinámica f=µ_k·mg es de sentido contrario a v_P.

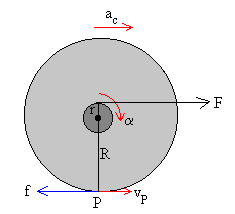Las ecuaciones del movimiento son

Para que a_c>a R, se tiene que cumplir que

• Si a_c<a R, entonces v_P<0. La fuerza de rozamiento dinámica f es de sentido contrario a v_P.

Las ecuaciones del movimiento son

Para que a_c<a R, se tiene que cumplir que

Casos posibles	Rodar sin deslizar	Rodar deslizando
0<r<R/2	vP=0, Fr<0	vP>0, f<0
r=R/2	vP=0, Fr=0	vP=0, f=0
R/2<r<R	vP=0, Fr>0	vP<0, f>0

Ejemplo

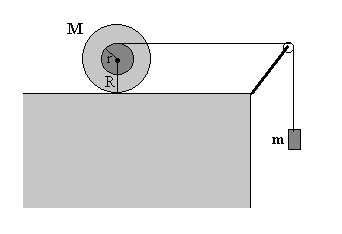Un cilindro de masa M y radio R tiene enrollada una cuerda en una hendidura de radio r<R, y de masa despreciable que la hace rodar sin deslizar a lo largo de un plano horizontal. La cuerda pasa por una polea y de su extremo cuelga un bloque de masa m. Determinar la aceleración del bloque y su velocidad cuando haya descendido h metros partiendo del reposo.

Dinámica

Tenemos que plantear las ecuaciones de la dinámica de dos cuerpos, el bloque y el cilindro.

Sobre el bloque actúan dos fuerzas la tensión de la cuerda y el peso. La ecuación del movimiento esmg-T=ma Las ecuaciones correspondientes al movimiento de traslación y al movimiento de rotación del cilindro son: T-Fr=mac RFr+rT=Ica

El momento de inercia de un cilindro es I_c=MR²/2. Si el cilindro rueda sin deslizar sobre el plano horizontal  a_c=a R

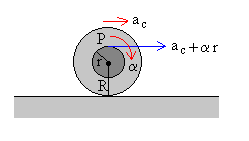Nos queda finalmente establecer la relación entre la aceleración del bloque a y la aceleración del centro de masas del cilindro ac. La aceleración del punto P es la suma de la aceleración debida al movimiento de traslación ac y la aceleración debida al movimiento de rotación a r

Completar en un papel las siguientes tablas:

Datos del problema

Masa del bloque, m	kg
Masa del cilindro, M	kg
Relación de radios r/R <1

Incógnitas

Aceleración del bloque, a	m/s2
Aceleración del c.m. de cilindro, ac	m/s2
Tensión de la cuerda, T	N
Fuerza de rozamiento, Fr	N

Una de las particularidades que se pueden observar es que la fuerza de rozamiento F_r no tiene una fórmula concreta ni tampoco su sentido está definido. Para unos valores del cociente r/R la fuerza tiene sentido positivo (por ejemplo, para r/R=0) y en otros caso tiene sentido negativo (por ejemplo para r/R=1). Existe incluso un valor para de r/R para el cual F_r tiene un valor nulo.

Así pues, la fuerza de rozamiento viene determinada por las ecuaciones del movimiento.

Balance de la energía

Cuando el bloque desciende una altura h partiendo del reposo, podemos determinar a partir de los cambios energéticos observados, la velocidad que alcanza el bloque o la velocidad del c.m. del cilindro.

• La energía potencial del bloque disminuye en mgh
• La energía cinética del bloque aumenta en mv²/2
• La energía del cilindro aumenta en Mv_c²/2+I_cw ²/2 (energía cinética de traslación del c.m. más la energía cinética de rotación)

El balance energético se expresa mediante la ecuación

Nos queda ahora relacionar la velocidad del bloque con la velocidad del c.m. del cilindro

v_c=w R es la condición de rodar sin deslizar. La velocidad del punto P es

¿Por qué no se incluye el trabajo de la fuerza de rozamiento en el balance energético?

Completar en un papel las siguientes tablas:

Datos del problema

Masa del bloque, m	kg
Masa del cilindro, M	kg
Relación de radios, r/R
Altura h que desciende el bloque	m

Incógnitas

Velocidad del bloque, v	m/s
Velocidad del c.m. de cilindro, vc	m/s